natural algorithms
I've been fascinated by natural algorithms for a while. They come up a lot in many aspects of nature, from anatomy of individuals to collective behaviours.
examples
fireflies

Fireflies are bioluminescent insects and use their lights for a variety of purposes. Some tropical fireflies synchronise their flashes perfectly when in large groups. It seems unbelievable that such small insects would be able to organise themselves to such accuracy.
The answer is, of course, simple. If you model each firefly as having a slowly increasing urge to flash that also increases each time a nearby firefly flashes, that is all that's required for order to be created from a huge swarm. People have demonstrated this by affecting the timing of real fireflies and by building a simple real-life model.
murmuration
I've spent many hours watching starlings flock. I'm not sure the reason they do this but you can get some very similar behaviour with a simple model, where each bird is modelled as a point moving in a direction that knows about nearby birds and follows some simple rules. I came up with something similar years ago when thinking about shoals of fish attacked by predators.

cellular automata
Some physical phenomena seems to have parallels in cellular automata. I wrote a bit about this in a previous blog post but there is more. From lizard skins to snail shells, I think there's a lot more to discover in this area.


I think the reason such a distinct appearance evolved on this snail may be that it's poisonous and wants potential predators to remember this.
ants

To me, ants are fantastic little automatons and seem to act like their own self-contained algorithms. Within a larger colony, they manage to create incredible complexity without much managing influence. We know that they communicate with pheromone trails and some people have had some success in replicating this ability with simple models.
Some organisms have also 'made use' of the simple ant, by creating a strange relationship with them. From trees that provide a perfect nest in return for protection, to a fungal parasite that appears to control the ant's mind for its own purposes.
hermit crabs

Hermit crabs are fascinating. They need to find a mobile home to fit into from the environment. There's a fascinating natural event in which hermit crabs gather around a new shell and line up in size order for a simultaneous shell swap when there is a complete chain.
It seems to me that this is a good fit for a natural algorithm causing emergent complexity. Crabs are known for their lack of cooperation and they may be following some simple rule instead; just grab the shell you want and fight others off.
I recreated this in code. The crabs are just circles and larger circles can barge others out of the way. They try to home in on the back the closest crab that is bigger than them but not too big. Plus some other tiny things like if a crab can't find another it likes then it will move around randomly.
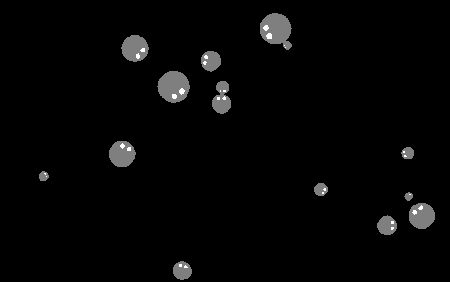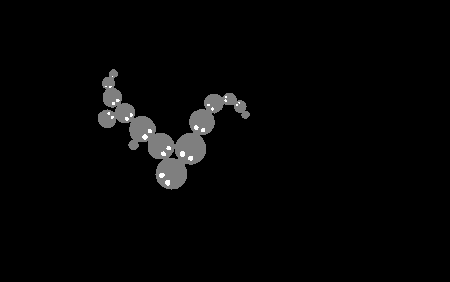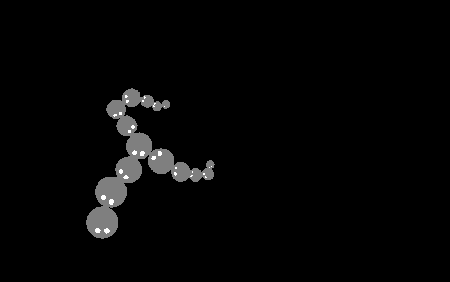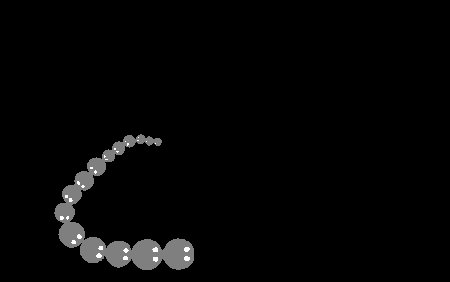

Success! I haven't simulated it all; there's no empty shell, no swapping and circles aren't crabs. But I have done enough to convince myself this is approximately correct. There's some interesting sorting behaviour that goes on when two partial chains meet too.

I've seen some other strange interactions when fiddling around with the parameters too. I wonder what emergent properties can be found with it. Maybe it's similar to Clusters.
speculation
All the algorithms here are extremely simple and it seems logical that certain small parts of the complex biological life on our planet could be thought of as simple algorithms. Perhaps it can be formally put as:
If something can be thought of abstractly as a simple system, then it will show some characteristics of that system.
This comes up a lot in maths too, for example a dartboard probability problem from a friend. He managed to conceptualize the problem as related to the volume of a cone which means that the answer also relates to it. This is also why π shows up in the solution to so many maths problems that don't seem to involve circles at first glance.
Maybe this is all trivial; you can use models to gain insight, big deal. It all ties into my world-view which I will write about... soon. There are other pre-requisite posts and many more diversions along the way though :)
attributions
Thanks to
-Greta Gaines for the firefly photo
-Llez for the hermit crab photo
-Steve Jurvetson for the ant photo
-Richard Ling for the sea snail photo
licensed under cc3.0
comments